#Algorithm #Algorithm_Graph #Algorithm_Tree #Algorithm_DFS #Algorithm_BFS

1. DFS, BFS?

그래프(, 트리)를 탐색하는 방법을 말한다.
DFS는 Depth First Search, BFS는 Breadth First Search를 의미하며, 단어의 뜻처럼 DFS는 주변보다는 하나의 경로에서 최대한 뻗어나가서 탐색하는 것이고, BFS는 주변부 부터 살펴나가서 범위를 점차 넓혀가는 탐색 방법을 말한다.

1-1. 사례

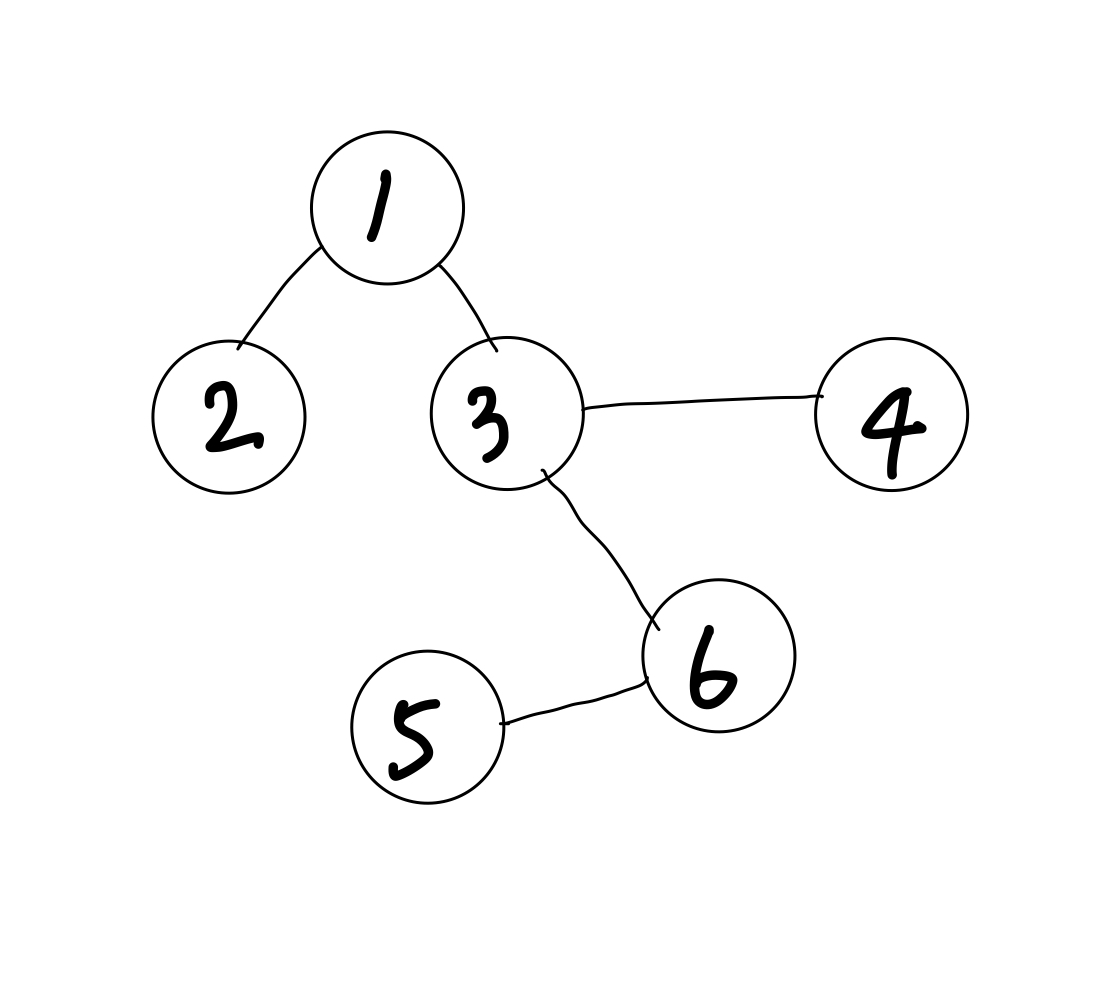
위의 그림을 DFS로 탐색한다면 (3을 시작점으로 가정),
하나의 경로로 끝까지 탐색한 후에 다른 경로를 찾는다고 했다.
3 -> 1 -> 2 까지 하나의 경로를 탐색한 후 다시 3으로 돌아와서
6 -> 5 그리고
4를 탐색하게 된다.

BFS로 탐색한다면 (3을 시작점으로 가정),
주변부 부터 탐색한다고 했다.
3의 주변부(간선으로 직접 연결되어 있는 것)인 1, 4, 6 먼저 탐색 후 그 각자의 주변부를 다시 탐색하여
1의 주변부인 2,
6의 주변부인 5를 탐색하게 된다.

2. 구현

아래는 그래프 예시 및 그래프 노드 클래스이다.

구현에서 검증할 그래프

                 -7 
 2   -3         /   
 |  / \       -4    
 | /   \    -/  \   
 1/     -6-/     \  
        /         -8
       /            
     5-

그래프 노드

package datastructure  
  
data class GraphNode(  
    val key: Int,  
    val neighbors: ArrayList<GraphNode?> = ArrayList<GraphNode?>()  
) {  
    companion object {  
        fun getDummy(): GraphNode {  
            val node1 = GraphNode(1)  
            val node2 = GraphNode(2)  
            val node3 = GraphNode(3)  
            val node4 = GraphNode(4)  
            val node5 = GraphNode(5)  
            val node6 = GraphNode(6)  
            val node7 = GraphNode(7)  
            val node8 = GraphNode(8)  
  
            node1.neighbors.add(node2)  
            node1.neighbors.add(node3)  
  
            node2.neighbors.add(node1)  
  
            node3.neighbors.add(node1)  
            node3.neighbors.add(node4)  
            node3.neighbors.add(node6)  
  
            node4.neighbors.add(node3)  
            node4.neighbors.add(node6)  
            node4.neighbors.add(node7)  
            node4.neighbors.add(node8)  
  
            node5.neighbors.add(node6)  
  
            node6.neighbors.add(node3)  
            node6.neighbors.add(node4)  
            node6.neighbors.add(node5)  
  
            node7.neighbors.add(node4)  
  
            node8.neighbors.add(node4)  
  
            return node1  
        }  
    }  
}

2-1. DFS 구현

DFS는 재귀와 스택으로 구현할 수 있다.
그래프의 경우 bi-direction에 사이클이 있는 경우도 있기 때문에 트리의 경우와 다르게 방문한 노드를 체크하는 로직이 추가로 필요하다.

재귀 사용

class DFS {  
    fun recursive(node: GraphNode, visitedNodes: MutableSet<Int?>) {  
        visitedNodes.add(node.key)  
        print("${node.key}, ")  
  
        for (neighbor in node.neighbors) {  
            if (neighbor != null && !visitedNodes.contains(neighbor.key)) {  
                recursive(neighbor, visitedNodes)  
            }  
        }  
    }
//...
}

스택 사용

class DFS {  
//...
    fun stack(node: GraphNode) {  
        val visitedNodes: MutableSet<Int> = mutableSetOf<Int>()  
        val stack = ArrayDeque<GraphNode>()  
        stack.add(node)  
        visitedNodes.add(node.key)  
  
        while(stack.isNotEmpty()) {  
            val curNode = stack.pop()  
  
            print("${curNode.key}, ")  
  
            for (neighbor in curNode.neighbors) {  
                if (neighbor != null && !visitedNodes.contains(neighbor.key)) {  
                    visitedNodes.add(neighbor.key)  
                    stack.push(neighbor)  
                }  
            }  
        }  
    }  
}

테스트

fun main(args: Array<String>) {  
    val node = GraphNode.getDummy()  
  
    val dfs = DFS()  
    dfs.recursive(node, mutableSetOf())  // 1, 2, 3, 4, 6, 5, 7, 8, 
    println("\n------------------------")  
    dfs.stack(node)  // 1, 3, 6, 5, 4, 8, 7, 2, 
    println("\n------------------------")  
}

2-2. BFS 구현

BFS는 Queue를 이용해 구현한다.

Queue 사용

class BFS {  
    fun bfsQueue(node: GraphNode) {  
        val queue: Queue<GraphNode> = LinkedList<GraphNode>()  
        val visitedNode = mutableSetOf<Int>()  
  
        queue.offer(node)  
        visitedNode.add(node.key)  
  
        while (!queue.isEmpty()) {  
            val curNode = queue.poll()  
  
            print("${curNode.key}, ")  
  
            for (neighbor in curNode.neighbors) {  
                if (neighbor != null && !visitedNode.contains(neighbor.key)) {  
                    queue.offer(neighbor)  
                    visitedNode.add(neighbor.key)  
                }  
            }  
        }  
    }  
}

테스트

fun main(args: Array<String>) {  
    val node = GraphNode.getDummy()  
  
    val bfs = BFS()  
    bfs.bfsQueue(node) // 1, 2, 3, 4, 6, 7, 8, 5,
    println("\n------------------------")  
}